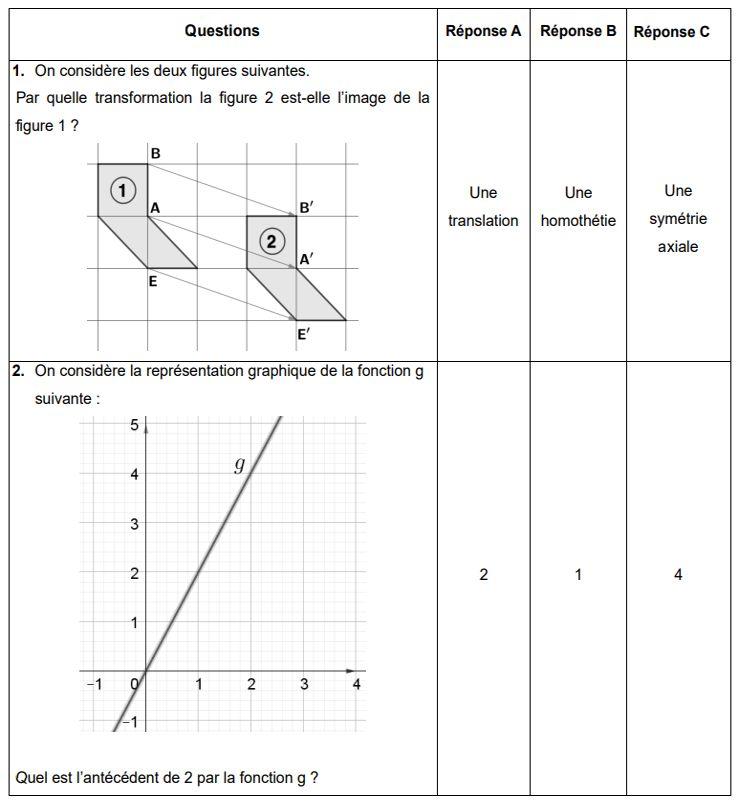
The college students took the math exam for the patent on Thursday, June 30th. Find the title.
After passing the French exam this morning, the third-graders passed the college patent math exam on Thursday afternoon, June 30th.
”Read more – Discover the results of the 2022 patent
More than 770,000 applicants from the general series have passed the exam, which lasts two hours and counts 100 points. Of the professional series, 85,309 students work in mathematics. Find topics.
Mathematics lesson in public course on Thursday, June 30th
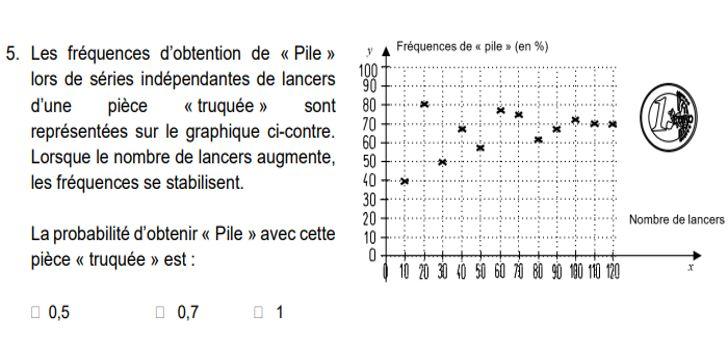
• dExercise 1 (20 points)
A family walks along the river. Kids want to know the width of the river. They take the symbols, count their steps and draw a map below, where points C, E and D, A, E and B are aligned. (The map is not for measuring.)
1. Prove that the lines (AC) and (BD) are parallel.
2. In the number of steps, determine the river width AC.
For the following questions, the length of a step is 65 cm.
3. CE length 13.3 m, show rounding to the nearest decimeter.
4. One of the children drops a stick into the river at point E. With current, the stick travels in a straight line to point C for 5 seconds.
Is. Calculate the velocity of the stick in m / s.
B. Is it true that “the stick moves at an average speed of less than 10 km / h”?
Exercise 2 (20 points)
This tutorial has multiple choice question papers (MCQ). No justification is required. For each question, three answers (A, B and C) are recommended. Only one answer is correct. Copy the question number and answer.
Exercise 3 (20 points)
A collector is counting on reselling his Pokemon cards.
There are 252 “Fire” type cards and 156 “Earth” type cards.
1.a Which of the following three propositions corresponds to the decay in the product of the major factors of the number 252:
B. Give the distortion in the product of the major factors of the number 156.
2. She wants to create identical decks, i.e. each has the same number of “Earth” cards and the same number of “Fire” cards.
Is. Can she pack 36?
B. What is the maximum number of pockets she can make?
How many cards of each type are there in each deck against?
3. She chooses a random card from all the cards. The cards are considered indistinguishable by touch.
Calculate the probability that this is an “earth” type card.
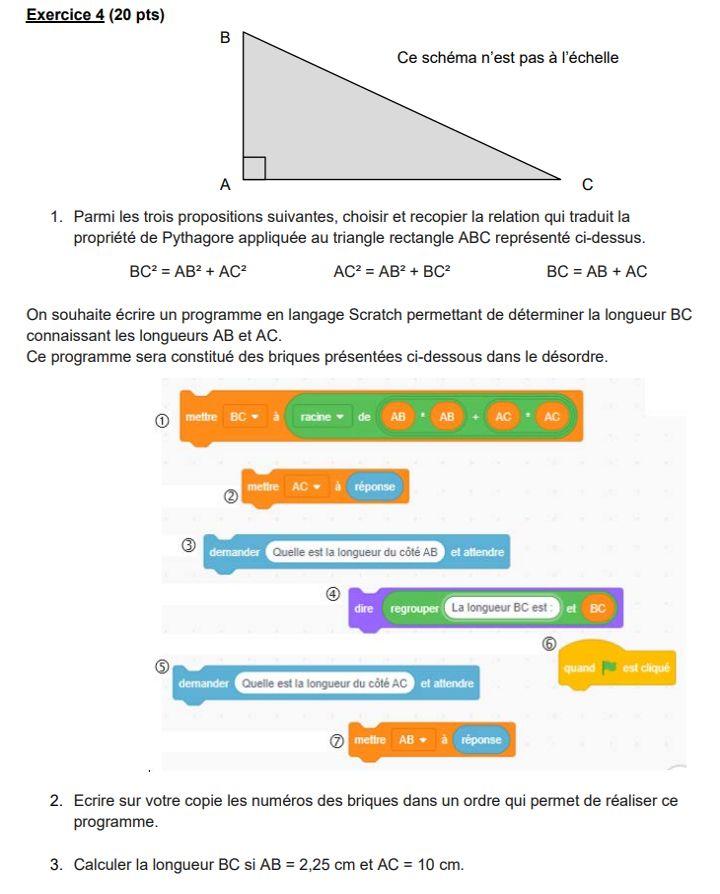
Exercise 4 (20 points)
In this exercise, x is definitely a larger number than 3.
We are interested in two geometric figures drawn below:
A rectangle with sides length x – 3 and x + 7;
x is a square of the page.
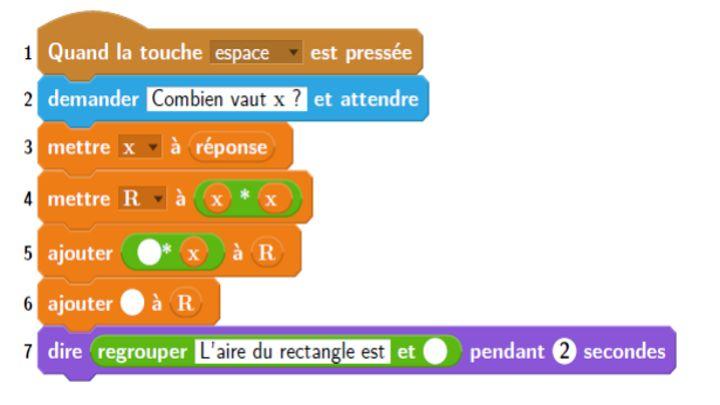
3. We have written the script below in scratch.
We want the program to return part of the rectangle when the user enters the value of x (strictly greater than 3).
Copy the contents of the three blank boxes of lines 5, 6 and 7, indicating the line numbers associated with your answers.
4. After pressing the space key we entered the number 8. What will the program return to?
5. Which number x should be chosen so that the area of the rectangle is equal to the area of the square?
Any trace of research, even if it fails, will be taken into account.
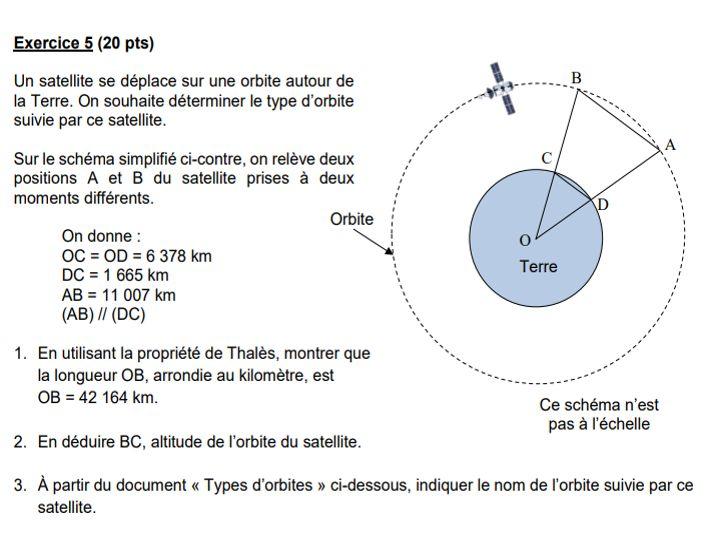
Exercise 5 (20 points)
In a home, water consumption is unusually high when water leaks.
We consider the following situation:
The bathroom is fitted with a cylindrical shaped basin as shown in the picture below.
The pipe will leak at the rate of one drop per second.
On average, 20 drops equals one milliliter (1 ml) of water.
1. Show that due to leakage, 86,400 drops fall on the bed in a whole day.
2. Calculate the amount of water that falls into the abyss in a week due to leakage in liters.
3. Show that the size of the basin is 18.85 liters, rounded to the nearest centiliter.
4. The drain of the basin is closed and the shelter has not been occupied for a week. Does the water in the ditch overflow? Justify the answer.
5. At the end of the 19th century, the per capita water consumption in France was about 17 liters a day. This was drastically increased by the generalization of piped water supply to households: it increased to 165 liters per day and in 2004 per citizen.
In 2018, French consumption is reduced to 148 liters of water per day and slightly per citizen.
Calculate the percentage of per capita daily water consumption that decreased between 2004 and 2018. This percentage is calculated up to the unit.
Answer Key (Public Sector)
Math lesson on professional patent on Thursday, June 30th
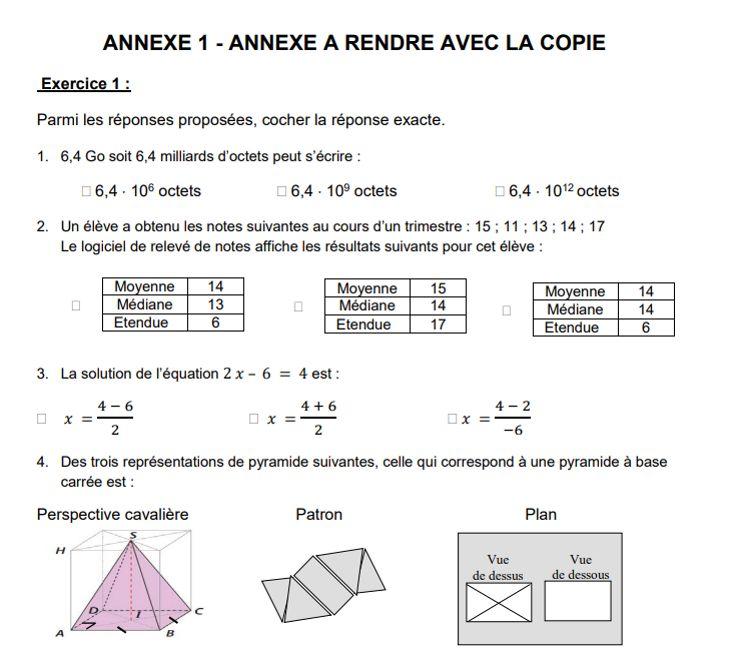
Exercise 1 (20 points)
The entire MCQ training should then be completed in Appendix 1.
Exercise 2 (20 points)
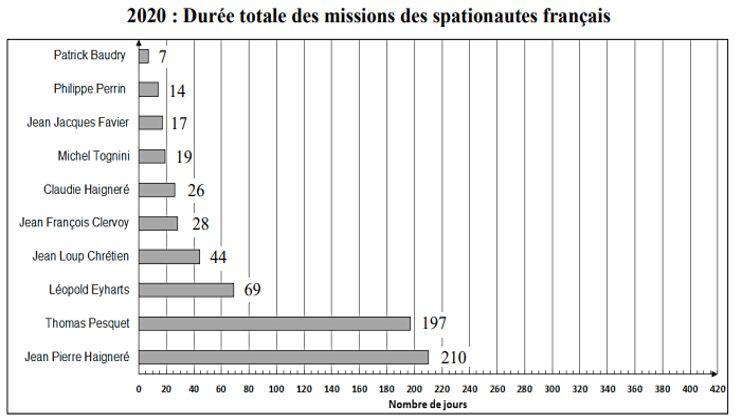
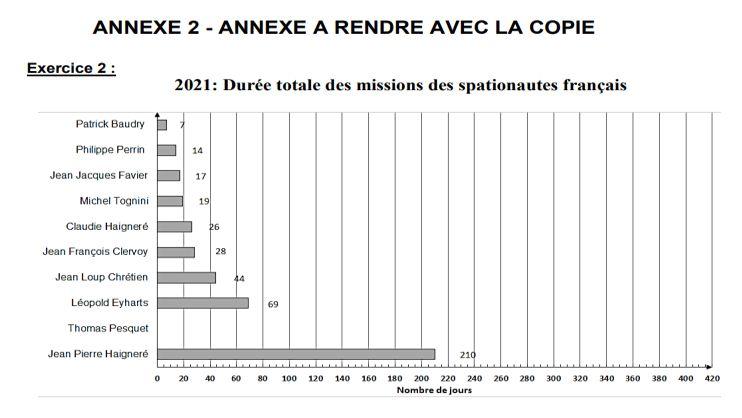
A document from 2020 provides the following information:
In 2021, Thomas Baskett completed his second 199-day mission. The purpose of the next two questions is to update the data in the document.
1. Determine the total duration of Thomas Baskett’s two assignments in the number of days.
2. Then complete the map in Appendix 2.
A journalist confirms that Thomas Baskett spent more than 40% of the total travel time of French astronauts in space.
3. Check the reporter’s claim.
Exercise 3 (20 points)
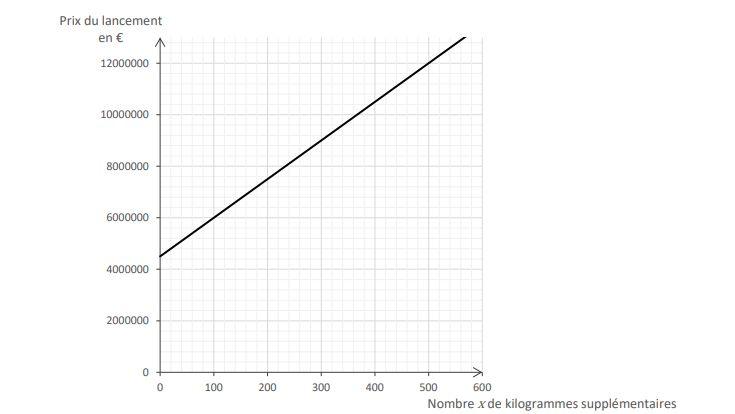
The launch cost of a satellite offered by an aerospace company is determined as follows: up to 4,500,000 euros up to 300 kilograms and an additional 15,000 euros per kilogram.
1. Check that the launch price of a satellite weighing 350 kg is 5,250,000.
We model the release price by the number x of extra kilograms by a function. The following diagram shows the representation of this function.
2. In the following three expressions, select the appropriate one for this function and copy:
f (x) = 15 000 x + 4 500 000 g (x) = 15 000 xh (x) = 50 000 x + 1 500 000
3. Specify whether the missile price of a satellite weighing more than 300 kg is proportional to the number x of the extra kilograms. Justify the answer.
4. A telecommunications company has a budget of ,000 8,000,000 to finance the launch of a satellite.
Is. Determine the maximum number of extra kilograms that can be started without exceeding this budget.
B. Reduce the maximum total weight of the satellite in kilograms on a budget of 8,000,000 euros.
Exercise 4 (20 points)
Answer Key (Professional)

“Proud explorer. Freelance social media expert. Problem solver. Gamer. Extreme travel aficionado.”